Portioning of the contents of a pack at home

The fvPortioning() function represents the portioning of a pack of frozen vegetables into a smaller unit. It is assumed that the microbial cells present in a contaminated pack are distributed into servings following a beta-binomial distribution, although the algorithm only retains one portion per pack (and not all the portions that can be obtained from a pack). The dispersion factor bPort represents the extent of cell clustering in the frozen vegetables within the package. The fact that the algorithm takes into account that a contaminated pack can produce a non-contaminated portion, enables the estimation of the prevalence of contaminated portions. It is assumed that the dispersion parameter and the number of portions (that can be obtained from a pack) are independent of the microbial numbers.

Usage

fvPortioning(
  data = list(),
  nLots = NULL,
  sizeLot = NULL,
  servingSize,
  unitSize = NULL,
  bPort
)

Arguments

data

a list of:

N

(CFU) A matrix of size nLots lots by sizeLot units representing the numbers of L. monocytogenes per pack before handling at home;

ProbUnitPos

Probability of (tested) individual lots being contaminated (vector);

P

Mean prevalence of contaminated lots (scalar).

nLots

Number of lots sampled or size of the Monte Carlo simulation (scalar).

sizeLot

Number of units or portions produced in a lot (scalar).

servingSize

(g) is the portion taken from a pack, which will later equals to the serving size (scalar or vector).

unitSize

(g) is the weight of a pack of frozen vegetables (scalar).

bPort

dispersion factor of cells within the package (scalar or vector).

Value

A list of three elements:

N

(CFU) A matrix of size nLots lots by sizeLot units representing the numbers of L. monocytogenes in the portions of frozen vegetables.

ProbUnitPos

Lot-specific probability of contaminated portions or servings (vector).

P

Mean prevalence of contaminated portions or servings (scalar).

Note

A dispersion factor \(bPort=1\) represents moderate clustering of cells Nauta (2005) in the frozen vegetables within the package.

References

Nauta MJ (2005). “Microbiological risk assessment models for partitioning and mixing during food handling.” International Journal of Food Microbiology, 100(1), 311--322. doi:10.1016/j.ijfoodmicro.2004.10.027 .

Author

Ursula Gonzales-Barron ubarron@ipb.pt and Regis Pouillot rpouillot.work@gmail.com

Examples

dat <- Lot2LotGen(
  nLots = 50,
  sizeLot = 100,
  unitSize = 500,
  betaAlpha = 0.5112,
  betaBeta = 9.959,
  C0MeanLog = 1.023,
  C0SdLog = 0.3267,
  propVarInter = 0.7
)
Nf <- fvPortioning(dat, servingSize = 150, unitSize = 500, bPort = 1)
str(Nf)
#> List of 12
#>  $ Lot2LotGenParameters:List of 9
#>   ..$ nLots       : num 50
#>   ..$ sizeLot     : num 100
#>   ..$ unitSize    : num 500
#>   ..$ betaAlpha   : num 0.511
#>   ..$ betaBeta    : num 9.96
#>   ..$ C0MeanLog   : num 1.02
#>   ..$ C0SdLog     : num 0.327
#>   ..$ propVarInter: num 0.7
#>   ..$ Poisson     : logi FALSE
#>  $ lotMeans            : num [1:50] 2.36 7.46 1.84 12.92 5.1 ...
#>  $ unitsCounts         : num [1:5000] 3.74 1.255 4.273 0.181 18.833 ...
#>  $ N                   : num [1:50, 1:100] 2729 530 983 2388 5954 ...
#>  $ ProbUnitPos         : num [1:50] 0.03465 0.05987 0.10991 0.00192 0.07998 ...
#>  $ P                   : num 0.0392
#>  $ betaGen             : num [1:50] 0.01996 0.06012 0.12523 0.00213 0.11932 ...
#>  $ nLots               : num 50
#>  $ sizeLot             : num 100
#>  $ unitSize            : num 500
#>  $ unitsServing        : num [1:5000] 12.467 4.183 14.244 0.604 62.777 ...
#>  $ servingSize         : num 150
#>  - attr(*, "class")= chr "qraLm"
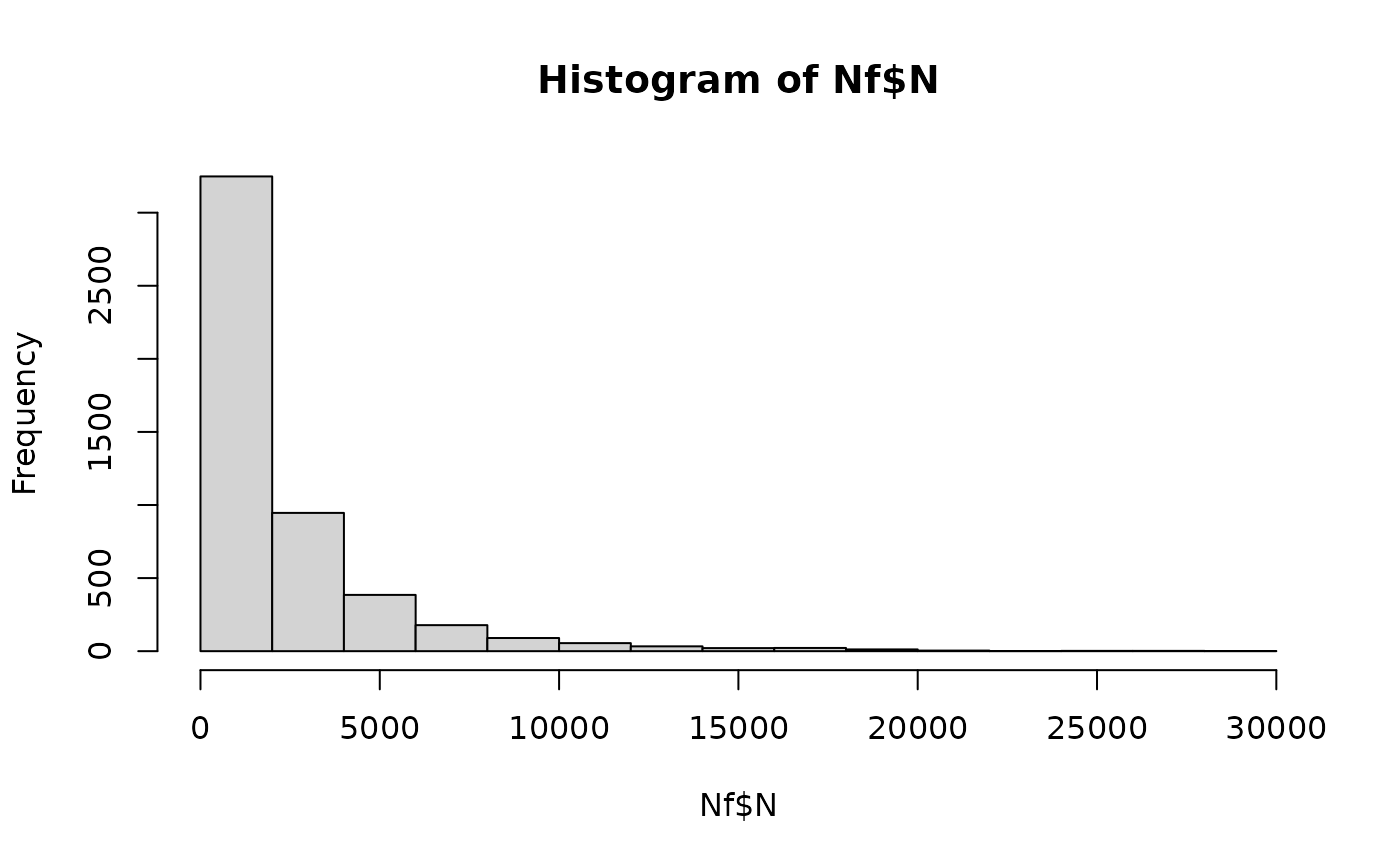
hist(Nf$N) # histogram of microbial cells in contaminated servings